一种基于面积的无线定位算法

文/山东科技大学信息与电气工程学院 李世光,李志文,王晓慧,韩旭

传统的无线定位算法受到非视距、多径干扰、信道噪声等因素的影响，无线定位精度往往不高。本文提出一种基于面积的定位算法。该算法以基站之间实际面积不变为基础，测量移动终端与各基站间的距离，通过误差处理，实现对移动终端的精确定位。仿真试验证明，该算法定位精度较高。

无线通信、微处理器技术的不断进步推动了无线定位技术的发展。近年来，无线定位技术在军事、智能交通、医疗管理、智能家居等多个方面得到了广泛的应用。对人们的生活带来了不可替代的作用。

1  概述

在无线定位算法中，场强定位算法最简单，但定位精度较差；AOA定位虽有一定精度，但接收设备较复杂；TOA定位精度较高，但对时间同步有较高要求；TDOA能消除对时间基准的依赖，可降低成本并保持一定的定位精度。但以上算法均不能降低不同信道上不同干扰。

基于面积的定位算法能够计算出实际面积与测量求得的面积误差，对误差进行处理后，能够降低各信道上的干扰。

2  基于面积的无线定位算法

为便于理解，将基站数量定位4个，分别位于边长为30m的正方形4个端点A、B、C、D处。移动终端P位于正方形内。平面分布图如图1所示。

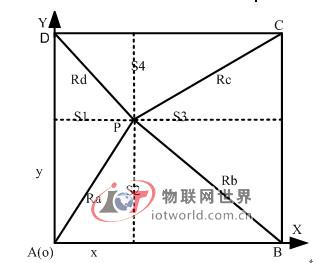
图1 平面分布图

Fig.1  The plane distribution map

通过采集基站的数据可以得到移动终端到基站A、B、C、D的距离，假设分别为Ra、Rb、

式中，

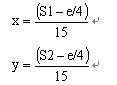
由于传输过程受到非视距、多径干扰、信道噪声等因素的影响，数据Ra、Rb、Rc、Rd中掺杂了各种噪声干扰，求得的△APB、△BPC、△CPD、△DPA的面积之和S不等于实际的正方形面积900，则可求出误差：

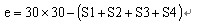
因为e是总面积的误差，将e等分为4份，则△DPA、△APB的面积误差约为e/4。再利用△DPA、△APB的边AD和AB均为30，可求出移动节点到正方形边AD、AB的距离为；

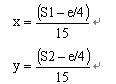
则（x y）就是经过误差修正后的点P的坐标。

为了进一步降低误差e对定位精度的影响，单位时间内增加采集次数，将求得的点P坐标取平均值。

3  实验仿真

根据以上原理进行MATLAB仿真，为方便观察，以y=5作为输入运动路径。在移动终端和4个基站的各信道上添加4个不同的随机噪声。仿真程序如下：

X=0:0.01:30;

n1=randn(size(X));

n2=randn(size(X));

n3=randn(size(X));

n4=randn(size(X));

Y=5;

Ra=sqrt(Y.^2+X.^2)+n1;

Rb=sqrt((30-X).^2+Y.^2)+n2;

Rc=sqrt((30-X).^2+(30-Y).^2)+n3;

Rd=sqrt(X.^2+(30-Y).^2)+n4;

R1=(Ra+Rd+30)/2;

R2=(Ra+Rb+30)/2;

R3=(Rb+Rc+30)/2;

R4=(Rc+Rd+30)/2;

S1=sqrt(abs(R1.*(R1-Ra).*(R1-Rd).*(R1-30)));

S2=sqrt(abs(R2.*(R2-Ra).*(R2-Rb).*(R2-30)));

S3=sqrt(abs(R3.*(R3-Rb).*(R3-Rc).*(R3-30)));

S4=sqrt(abs(R4.*(R4-Rc).*(R4-Rd).*(R4-30)));

e=S1+S2+S3+S4-900;

x=(S1-e/4)./15;

y=(S2-e/4)./15;

for i = 1:2950  %对每50个数据均值

    sum = 0;

    for j = i : i+49;

       sum = sum + x(j);

    end

    x(i) = sum /50;

end

for i = 1:2950

    sum = 0;

    for j = i : i+49;

        sum = sum + y(j);

    end

    y(i) = sum /50;

end

plot(x,y,'*');

进行误差处理的MATLAB运动轨迹仿真图和未进行误差处理的MATLAB运行轨迹仿真图如图2和图3所示。

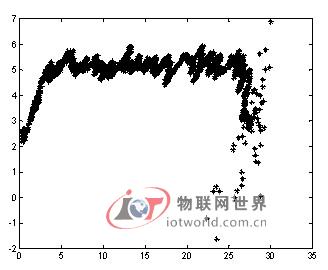
图2 误差处理后的MATLAB运动轨迹仿真图

Fig.2  MATLAB trajectory simulation map error after treatment

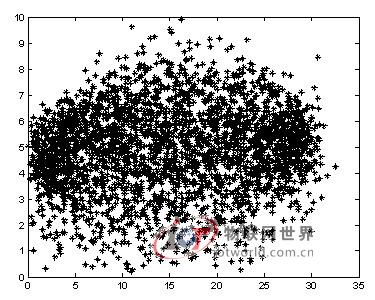
图3 未进行误差处理的MATLAB运动轨迹仿真图

Fig.3  No MATLAB trajectory simulation map error processing

由图2和图 3可以看到，求得的点P坐标进行误差处理后能有效地减弱各信道上的噪声干扰，提高系统的定位精度。

由图2可以看出，当x值较小或较大时，由于无法充分对求得的坐标求均值，坐标数值浮动较大。由此可知单位时间内对数据的采集次数越多，求均值的坐标组数越多，数据的浮动越小，定位越准确。

4  结束语

本文提出了一种基于面积的无线定位算法，并利用Matlab仿真软件进行了仿真。实验结果表明，该算法能在各信道中存在不同干扰的情况下，得到测量的总面积与实际总面积的误差，对误差进行处理后能有效的降低干扰对定位系统的影响，提高定位的精度。

基金项目：山东科技大学2012-2013年度研究生科技创新基金项目。